М.И. Розно
 В этом материале рассмотрим более подробно СПК по альтернативному признаку.
В этом материале рассмотрим более подробно СПК по альтернативному признаку.
Пусть задан план одноступенчатого СПК по альтернативному признаку:
n=100 – объем выборки;
Ас=1 – приемочное число.
Это значит, что из партии нужно случайным образом взять 100 изделий и проконтролировать их по принципу «годен – не годен». Если число обнаруженных в выборке негодных изделий d ≤ Ас=1, (т.е. d=0 или d=1), то партию следует принять, а если d>1, то – забраковать.
При двухступенчатом плане СПК по альтернативному признаку план контроля состоит уже из 5 параметров, которые, например, равны:
n1 = 100 – объем 1-ой выборки;
Ас1 = 0 – приемочное число для 1-ой выборки (1-ой ступени СПК);
Re2 = 2 – браковочное число для 1-ой выборки;
n2 = 200 – объем 2-ой выборки;
Ас2 = 2 – приемочное число для 2-ой ступени СПК.
При этом правила проведения СПК и принятия решения «о судьбе» партии таковы:
отбираем случайно 1-ю выборку объёмом n1 = 100 изделий и контролируем их;
если обнаруженное при этом число негодных изделий d1:
d1 ≤ Ас1 – то сразу принимаем партию (в данном случае при d1=0);
d1 ≥ Re2 – то сразу бракуем партию (в данном случае при d1≥2);
Ас1< d1 < Re1 – то переходим ко 2-ой ступени СПК, т.е. берем 2-ю выборку (в данном случае это происходит при d1=1);
если после контроля 2-ой выборки суммарное число обнаруженных негодных изделий в 1-ой и во 2-ой выборках (d1 + d2):
(d1+d2) ≤ Ас2 – то принимаем партию (в данном случае при d1+d2≤2);
(d1+d2) > Ас2 – то бракуем партию (в данном случае при d1+d2>2).
Как уже говорилось, при любом конкретном плане СПК для любой конкретной партии продукции с известным уровнем дефектности результат контроля нельзя предсказать однозначно, все зависит от «везения» при случайном взятии выборки (исключая тривиальные случаи, когда в партии совсем нет негодных изделий или наоборот, все изделия негодные). Но при этом можно рассчитать вероятность того, что партия с известным уровнем дефектности будет принята при СПК с данным планом контроля. Естественно, что вероятность приемки партии будет зависеть от уровня дефектности: чем он больше, тем меньше вероятность (шансы) успешно пройти контроль. Таким образом, каждому плану СПК однозначно соответствует оперативная характеристика (ОХ), т.е. характеристика, показывающая зависимость вероятности («шансов») приемки партии от группового показателя качества, в данном случае – от истинного уровня дефектности в контролируемой партии (совокупности). Эта зависимость для СПК по альтернативному признаку всегда убывающая.
ОХ показывает, с какими «шансами» партия продукции пройдет через контроль, если эта партия имеет определенный уровень дефектности. Так, для плана контроля с ОХ, изображенной на рис.4, партии с уровнем дефектности q=1% пройдут через контроль с вероятностью P=0,95, т.е. для одной такой партии это – «шансы» пройти контроль. А для многих таких одинаковых партий 95 из 100 из них пройдут контроль, а 5 партий будут забракованы, хотя все партии одинаковы: каждая имеет q=1% дефектных изделий. А при уровне дефектности 7% для одной партии шансы приемки P=0,2, а для многих таких партий только 20 из 100 из них пройдут контроль, а 80 партий будут забракованы.
Для любого конкретного плана СПК можно указать «характерные» точки на ОХ (см рис.4):
qпр – приемочный (сравнительно «хороший») уровень качества (в данном случае – низкий уровень дефектности), при котором партия имеет «высокие шансы» P=1-α быть принятой (α – риск изготовителя);
qбр – браковочный (сравнительно «плохой») уровень качества, при котором партия будет иметь весьма «низкие шансы» P=β быть принятой (β – риск потребителя);
q0,5 – «безразличный» уровень качества, при котором с «шансами» Р=0,5 партия может быть принятой.
Естественно, разные планы СПК имеют существенно разные кривые оперативных характеристик, но всегда qпр<q0,5<qбр (если только установленные риски α и β меньше 0,5). Конечно, разработчики стандартов по СПК рассчитывают ОХ всех планов, приводимых в стандартах, но пользователь этих планов не видит ОХ, поэтому действует «по слепой вере». Но ведь ответственность за качество сегодня возложена на изготовителя. А если речь идет о потребителе контролируемой партии, то ему тоже необходимо знать, «что же делает» его входной контроль. Вряд ли сегодня разумно действовать «вслепую», нужно именно видеть ОХ, чтобы оценить «здравый смысл» применения данного СПК. Поэтому знание величин qпр, q0,5 и qбр для известных рисков α и β позволит пользователю «увидеть ОХ» хотя бы в трех точках и оценить возможности данного плана контроля.
В самом деле, если изготовитель, зная свое производство, абсолютно уверен, что уровень дефектности в производстве никогда не поднимается выше 1000 ppm = 0,1%, то какой же смысл применять СПК с приемочным уровнем qпр = 0,2%? Такая продукция практически всегда уверенно пройдет через контроль (см. по аналогии с рис.4). В другом случае, если потребитель знает, что уровень дефектности 2000 ppm = 0,2% – это заведомо неприемлемый для его производства уровень дефектности закупаемых комплектующих изделий, то какой смысл при входном СПК применять план контроля с q0,5 =0,3% = 3000 ppm? Ведь такой контроль в половине случаев пропускает партии с уровнем дефектности 3000 ppm, а значит, партии с уровнем дефектности 2000 ppm = 0,2% будут приниматься более чем в половине случаев.
К сожалению, подобные случаи часто приходится видеть в производстве. И на вопрос «Почему же вы применяете такой план СПК?» звучит ответ: «А такой план в ГОСТе на нашу продукцию» или «Так у нас записано в контракте на поставку». Нетрудно понять, что кроме впустую затраченного труда применение такого СПК не дает ничего.
Как же «увидеть» ОХ? Легче всего воспользоваться специальными программными продуктами, например, пакетом QStat [3]. Этот пакет позволяет анализировать, а также подбирать (синтезировать) наилучшие для данной конкретной ситуации одно- и двухступенчатые планы СПК по альтернативному признаку. На рисунке 5 представлены построенные для примера оперативные характеристики трёх разных планов СПК: одноступенчатого (n=50; Ac=0) и двух двухступенчатых (первый: n1=75; Ac1=0; Re1 =2; n2=150; Ac2=2; второй: n1=100; Ac1=0; Re1 =2; n2=200; Ac2=2) для партий объема N=1000.
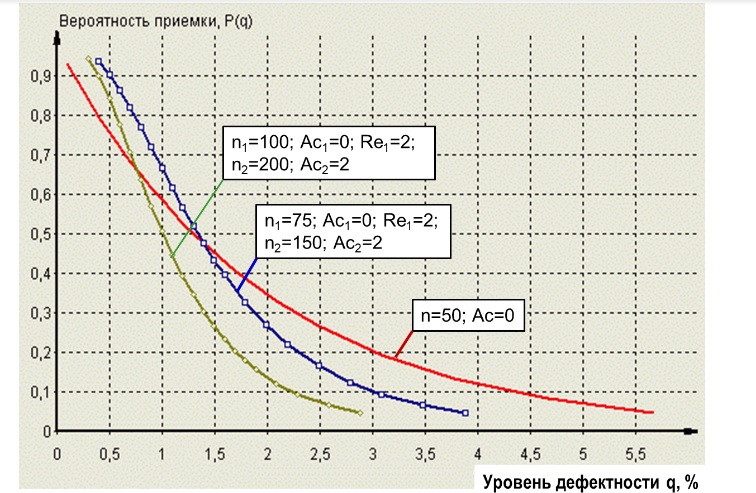
Рис.5. Оперативные характеристики трех планов СПК по альтернативному признаку
