М.И. Розно
Во многих производствах часто применяется одноступенчатый СПК с приемочным числом Ас=0, а объём выборки значительно меньше объёма партии (n≤0,2N). При этом оперативная характеристика становится похожей на убывающую экспоненту (см., например, ОХ для плана n=50; Ac=0 на рис.5), и могут быть предложены простые приближенные формулы для расчета характерных точек на оперативной характеристике. Именно такие планы с Ac=0 допускаются при работе по стандарту IATF 16949.
Практический интерес представляют три точки на оперативной характеристике, соответствующие вероятностям приемки: P=0,95; P=0,5 и P=0,1. Им соответствуют три уровня дефектности: qпр=q0,95; q0,5 и qбр=q0,1. Иначе говоря:
- при первом (приемочном) уровне дефектности qпр=q0,95 партии продукции будут весьма уверенно приниматься (с вероятностью P=0,95, т.е. только одна из 20 партий с таким q=qпр будет случайно отклоняться);
- при втором («безразличном») уровне дефектности q=q0,5 в половине случаев партии будут приниматься, а в половине – отклоняться;
- при третьем (браковочном) уровне дефектности qбр=q0,1 партии продукции будут достаточно уверенно отклоняться (будут приниматься с малой вероятностью P=0,1, т.е. только одна из 10 партий с таким q=qпр будет случайно проходить через контроль).
Приведём простые приближенные формулы для этих трёх уровней дефектности, которые зависят от объема применяемых выборок n:
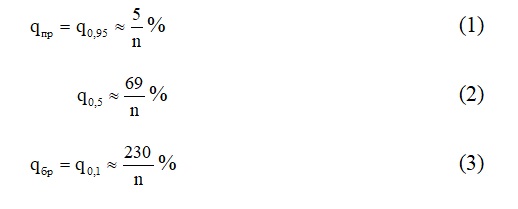
Эти формулы были получены путем приравнивания вероятности приемки партии (случай ) по биномиальному распределению [4] соответственно к величинам 0,95; 0,5 и 0,1. Далее полученные уравнения решались относительно значения q с помощью разложения функции в ряд Тейлора. Для удобства пользования значения q в формулах (1) – (3) даны в процентах.
Формулы (1) – (3) имеют достаточную точность, если объем выборки n не превышает 1/5 объема партии и если n ≥5. Проанализируем результаты расчетов по формулам (1) – (3) на численных примерах.
Пример 1. В соответствии с требованием стандарта IATF 16949 для контроля продукции поставщик применил статистический приемочный контроль по альтернативному признаку с Ac=0. При этом установлено, что из каждой партии объема N=500 берется выборка n=70, и в ней не допускается ни одной дефектной детали. При каком уровне дефектности партии будут уверенно задерживаться таким контролем? Т.е. какая будет величина браковочного уровня дефектности? – По формуле (3) получаем: q=(230/70)≈3,3%. А по формуле (2) получается, что партии с уровнем дефектности q=(69/70)≈1% в половине случаев успешно пройдут через такой контроль. Интересно было бы спросить у потребителя, устроят ли его такие «гарантии качества»?
Пример 2. На предприятии каждая партия закупаемых комплектующих изделий проходит входной выборочный контроль по плану: объем выборки n=30; приемочное число Ac=0. Какой уровень дефектности будет уверенно «отсекаться»? – По формуле (3) получаем: q=(230/30)≈7,7%. А партии с уровнем дефектности q=(69/30)=2,3% в половине случаев будут успешно приняты (см. формулу 2). А хорошо ли это для последующего сборочного производства?
Пример 3. В технологии записано: «После наладки оборудования изготовить и проверить первые 10 деталей. Если все они окажутся годными, можно начинать серийное производство».
По сути, такое требование означает применение статистического приемочного контроля с планом (n=10; Ac=0) для начала производства. Каково назначение этого контроля? – Очевидно, убедиться, что налаженное производство обеспечивает достаточно низкий (в идеале – нулевой) уровень дефектности. Но давайте посмотрим, какой же уровень дефектности при этом гарантируется? В соответствии с формулой (1) с хорошей уверенностью производство будет одобрено, если уровень дефектности q=0,5% (или менее). Но при каком относительно высоком (браковочном) уровне дефектности производство будет приостановлено? – На этот вопрос отвечает формула (3): при уровне дефектности q=(230/10)=23% (или более). А по формуле (2) получаем: при уровне дефектности q=(69/10)=6,9% производство будет одобрено в половине случаев. А устроят ли такие проценты дефектности организаторов производства?
Как известно, для современной сложной техники необходим очень низкий уровень дефектности, порядка единиц-десятков ppm, не более, иначе мы «захлебнемся в неприятностях» [5]. Тогда естественно задать вопрос: А какой же план СПК по альтернативному признаку следует установить (при Ac=0), чтобы контроль уверенно «отсекал» партии с уровнем дефектности, например, 100 ppm=0,01%? Для ответа на этот вопрос приравняем формулу (3) к значению 0,01% и получим: n=23000, и это – выборка! Аналогично, приравняв формулу (2) к тому же значению 0,01%, получим результат: при выборке n=6900 и Ac=0 соответствующий СПК будет в половине случаев принимать партии продукции с уровнем дефектности 100 ppm=0,01%. Даже если объемы партий позволяют брать такие выборки, то вряд ли такой СПК экономически целесообразен. А если объем выборок уменьшить при Ac=0, то СПК неизбежно будет пропускать партии с более высоким уровнем дефектности.
К еще одному недостатку планов контроля с Ac=0 следует отнести слишком большую разницу между браковочным qбр и приемочным qпр уровнями дефектности, как видно из формул (1) и (3), относительная разница составляет 46 раз! А диапазон значений уровней дефектности между qпр и qбр – это «зона неуверенной работы» СПК, в которой относительно велика «роль случайности», а не действительное качество партии: здесь партии «не очень уверенно» принимаются, но и «не очень уверенно» отклоняются.
Если же приемочное число Ac сделать больше нуля, или применить двухступенчатый план СПК, то при том же объеме выборки оперативная характеристика поднимется выше при всех значениях q, т.е. СПК будет принимать (пропускать) партии с более высоким уровнем дефектности. Именно поэтому стандарт IATF 16949 разрешает только планы СПК с Ac=0. Однако и планы СПК с Ac=0, как мы убедились, не обеспечивают «оптимистических результатов» при приемлемых объемах выборки.
Заключение:
СПК по альтернативному признаку не даёт уверенных результатов для потребителя в качестве «заслона» от продукции с повышенным уровнем дефектности. Даже при выборках в сотни единиц СПК может пропускать партии продукции с уровнем дефектности десятые доли процента.
СПК по количественному признаку может дать лучший результат, здесь возможно обеспечение уровней дефектности порядка 0,1% при объеме выборки десятки единиц.
Но свойства СПК ухудшаются при контроле смешанных партий, состоящих из разнородных производственных партий, что вполне может происходить при производстве и поставках деталей и узлов на сборочные заводы. По этой причине современные требовательные заводы, например, автосборочные предприятия, как правило, совсем отказываются от входного контроля партий закупаемых узлов и комплектующих изделий, но организуют работы по обеспечению качества на заводах-поставщиках.
Более уверенное качество производства и поставок изделий может обеспечить статистическое управление процессом (SPC), тогда при небольших затратах на контроль выборок продукции удается обеспечить даже более уверенные гарантии качества для потребителей, чем при сплошном контроле. Но любое применение статистических методов в производстве требует определенной статистической грамотности от персонала и соответствующего обучения.
Литература
1. Касторская Л.В. Управление качеством – используемые подходы и необходимые данные. https://erp-corp.ru/expert/quality_concept/
2. Розно М.И. Статистический приемочный контроль качества продукции: свойства и возможности. – Контроль качества продукции, №№ 9, 10, 2020 г.
3. Лапидус В.А., Розно М.И. и др. Статистический контроль качества продукции на основе принципа распределения приоритетов. /Лапидус В.А., Розно М.И., Глазунов А. – М., Финансы и статистика, 1991. – с. 186-196.
4. Биномиальное распределение: http://statistica.ru/glossary/general/binomialnoe-raspredelenie/
5. Розно М.И. Откуда берутся «неприятности». – Стандарты и качество, № 11, 2002.